nivek
As Above So Below
This is a report I came across today, its quite interesting, pointing out a reflection of the house on the UFO is brilliant...
A Re-evaluation of the Balwyn UFO Photograph
By Francois Beaulieu
Introduction:
On April 2, 1966, at about two in the afternoon, a young Australian businessman by the name of James Kibel went outside of his house to take a few pictures. He owned an early Polaroid camera loaded with instant roll film that hadn't been used in a couple of years. The film was long past its expiry date, but he thought he'd nonetheless try and finish the roll by taking a few snapshots in his garden.
However, shortly after he went out, his attention was drawn to something unusual in the sky. He observed a silver metallic object that rapidly came in his direction and briefly hovered near his house. At that point, he had the presence of mind to raise his Polaroid camera and take a quick snapshot. The resulting picture soon ended up in various publications and holds the distinction today of being one of the most controversial UFO pictures ever taken.
This picture has been examined more or less closely over these many years and I had the recent opportunity to re-examine all that had been written about it and compare it against a recent scan of the actual print. This then is my re-evaluation of the Balwyn photograph.
My background
I became interested in UFOs at age six (in 1960). At age 8, I got my first UFO book. It contained several very realistic photomontages to illustrate some of the cases presented. At the time, I wasn't quite sure what photomontages were, but I could tell that there was something not quite right about those images. From that point on, I became suspicious of any photograph claimed to be that of a real UFO…
In the summer of 1967, I set out to do a series of tests to see if I could reproduce some of the UFO photographs I saw in popular UFO magazines of the period. My father happened to own a Polaroid Land 100 camera and I decided to use it to conduct the tests.
Polaroid Land film was the "peel-apart type". This was a type of film that contained the processing chemicals in a pocket at one end that was spread over the photographic paper when the film was pulled through two rollers at the side of the camera. I shot quite a lot of pictures using this camera during that time - not only of UFO models, but also of family members. And I still have these to this day. Thus, I am quite familiar with the behaviour of Polaroid film of that period. Flaws in the prints were very common due to the unpredictability of the film processing. Variations in temperature, how fast the film was pulled out of the camera and how the film was peeled apart could all affect the final appearance of the print.
The camera my father owned:

The peel-apart film:

One of my photos taken in August 1967 of a small UFO model (note the print flaws):

My experiments with the Polaroid camera eventually led to a lifelong passion for photography, which eventually led to research in three-dimensional media, which became my specialty up to the present day.
The Balwyn picture
I first came across the Balwyn picture shortly after it was taken. In those days, I visited newsstands quite regularly in search of any magazine that contained articles on UFOs and one day, I was amazed to find a special issue on the subject released by the well-known American magazine "LOOK". This was in 1967. This special issue (titled appropriately enough "Flying Saucers") contained several colour photographs of UFOs and, on page 34 appeared one particularly intriguing daylight picture showing an airborne object shaped like a bowl on its side and having a golden shade. The object appeared to be hovering over a house. I remember being fascinated by the picture but not having any opinions as to its authenticity. The picture was said to come from an anonymous source and looked fairly clear and sharp.


Many years later, looking back at this picture (yes, I still have a copy of that magazine in my files), I realize now that the reason why the object looked gold was most likely because it was a snapshot taken of the original print with daylight film under tungsten lighting.
Over the years, I saw the Balwyn picture reproduced multiple times in various magazines, mostly in black & white and in lower definition than the initial picture from LOOK magazine.
It was only a few years ago that I came across a better reproduction of this picture on Bill Chalker's website - thanks to a recent scan made of the original print. It showed the full image area in the original colours - revealing that the object was a silver colour, not the golden shade apparent on the original LOOK reproduction.

I was impressed to discover that the person who had taken that picture was now identified, was still alive and still had the original print in his possession.
I thus decided to do more research on this print and soon discovered that it was considered quite controversial. One of the points that was brought up was that one could see a reflection of the roof of a house on the surface of the object. According to the person who brought this up, this was, in his opinion, proof that the object was close to the photographer since he reasoned that the person taking the photograph was on the same side of the house as the object. In his opinion, the object was then most likely a very small object close to the camera.

The next controversy that was brought up was that there was what looked like a zigzag pattern or line of discontinuity on the original print, which some claimed was an indication that the picture was in fact a second generation photograph showing a composite of two distinct pictures.
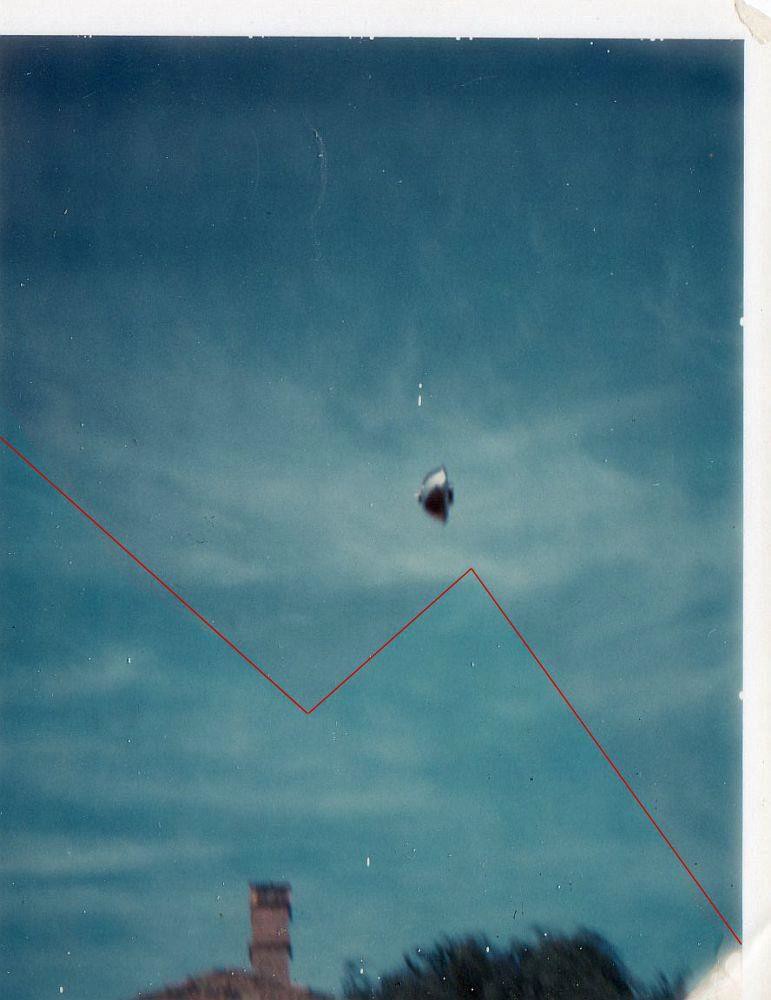
So let's address the first point:
At the time when it was realized that the surface of the object reflected the roof of a house, we had not found the actual location where the picture was taken. After the actual house was located and that satellite pictures of it were examined, it was realized that the only way for that picture to have been taken was for the object to be on one side of the house and the photographer to be on the other side of the same house. This is because the object reflects one side of the house, but the roof and chimney that appear in the lower portion of the picture are of that same house, which means that the photographer had to be on the other side. The initial argument was based on the premise that the photographer was on the same side of the house as the object (and therefore the object may have been close to the photographer) and that the roof and chimney appearing at the bottom of the picture were that of a neighbouring house. But that has proven not to be the case.
It was also suggested by some that, although the photographer was clearly located on the left side of the house, the object might have been a small object on the same side and the reflection could be that of a house behind the photographer. However we found no such house in that location.
The reflection of the house appearing on the object and the roof and chimney appearing at the bottom of the picture are clearly of the same house. This means that the object had to be some distance away from the photographer and thus had to be fairly large…

Comparing Paul Dean's picture of the roof of the house from the left side with the roof as it appears in the original picture:

Now let's address the second point:
Several people pointed to a zigzag line that appears about the middle of the picture and seems to delineate what looks like a difference in exposure between the top and bottom of the picture. This apparent difference takes the form of a slightly greyish cast on the top part of the picture and is most apparent on the recent scan made of the print.
Some have suggested that this proves that the Balwyn photograph is in fact a composite of two pictures that were cut with a pair of jagged-edged scissors and glued together.
This explanation is questionable for a number of reasons. First of all, Polaroid prints of the period tended to warp very rapidly. They would warp within minutes of being laid flat on a table. It would have been very difficult to mount two such prints and not reveal their cut edges quite clearly. In fact, even with a normal print, the edges of each image would still be very clearly defined.
I in turn suggested that a similar effect might have more easily been produced using a double exposure technique. Polaroid cameras of that period were designed in such a way that more than one exposure could be made before the film was pulled out of the camera for processing. Thus, a lens cap with a zigzag pattern cut-out could in theory have been used to accomplish such an effect.
However, even if either of the above techniques had been attempted, there would have been a major hurdle in creating such a hoax: As was mentioned above, the object in the picture reflects back into the camera's lens an image of the roof of the house. To create a hoax, a metallic bowl of sorts would have had to be thrown in the air and photographed just at the right moment. The likelihood that a bowl thrown up in the air would position itself in a way where it would reflect the roof of the house back into the lens of the camera is quite slim and could not be seen by the photographer until after the photograph was processed. Therefore, an enormous number of attempts would have had to be made in order to hopefully get a single picture that matches this requirement. This would have been quite a feat to accomplish. Yet the photographer himself never even brought up the matter of the object reflecting the roof of the house.
The problem with all the theories above (including my own) is that they do not match what actually appears on the scan of the print when it is examined closely.
One thing I knew from the days I used a Polaroid camera with peel-apart film was that the chemicals often spread unevenly on the print, which resulted in what looked like an unevenly exposed print. This became worse when the film had passed its expiry date, as the chemicals would tend to dry out and not spread over the entire length of the print.
Here is an example:

Looking closely at the scan of the Balwyn picture, it shows all the signs of a print that was exposed after its expiry date.
First, the top edge of the image shows a darker sky colour. Then there is that zigzag pattern suggesting that some chemicals had run out as the print was pulled out of the camera. Similar zigzag patterns have been observed on other Polaroid prints.
Here is an example:

On the Balwyn print, one can see that the top section (above the zigzag) has a greyish tinge. But what is most telling is that, at the bottom right edge of the print, one can see the greyish chemicals widening up again as they reach the right edge and then completely run out. The characteristic observed at the bottom right edge effectively proves that the zigzag line was indeed caused by the chemical spreading unevenly and not by any manipulation of the print or of the exposure.

Now, compare this to (where the chemicals similarly run out completely at one edge):

Other observations
I would like to add here that the claim of this being a photograph of a photomontage is weakened even more when one examines the camera used to take the picture.

In order to photograph a photomontage, a very precise alignment and focusing of the camera is necessary. The problem here is that a camera such as the Polaroid 800 does not have a viewfinder that allows such alignment and focus at close range due to the wide parallax discrepancies between the lens position and the viewfinder position. Therefore, it would have been extremely difficult to align and focus such a camera on a small composite made up of two prints - not to mention properly lighting it.
One could of course suggest that the original is not a Polaroid print. However, the current scan shows all the flaws typical of Polaroid prints of the period - flaws that did not appear on regular processed prints. Also, a recent scan showing the jagged edges of the print proves that the original print is indeed of the type used in Polaroid 800 cameras, which the photographer says he used. The film name is Polaroid Land Picture roll type 48.

Here a scan of the Balwyn print showing the jagged edges typical of Polaroid roll film compared to a period print made with the same Polaroid roll film (in its b&w version - type 47):


Therefore it is clearly established that the original Balwyn print was made using Polaroid roll film of the period which can only be loaded in specific early sixties Polaroid roll film cameras such as the model 800. None of these models had features that would allow easy photo duplication or manipulation.
Another point worth noting: When the witness saw the object, he described it as being in an upright position. However, just as he was about to take the picture, he claims that the object unexpectedly flipped on its side and, as soon as the picture was taken, it flipped back to its original orientation. This bizarre manoeuvre puzzled the witness. Yet it is in fact the reason why the surface of the object in the picture reflects the roof of the house. Had the object remained in an upright position while the picture was taken, it would have only reflected the sky and clouds above it and thus, no clue would have appeared on the picture as to its distance from the camera.
Conclusion
I have no doubt after studying the scan of this print for over a year that the picture is a single exposure of the actual scene taken with a Polaroid camera dating from the early sixties and that the object in the picture was airborne and most likely of significant size. Of course, the nature and origin of the object remain unknown.
Taking the analysis further
One problem we have at the moment is that the scan of the original print is of low resolution and in a compressed format (jpg). We would need a scan to be from eight to sixteen times higher resolution and in uncompressed format (tif or bmp) in order to reveal more detail in the print.
The first problem we encounter with the current scan is that magnification of the image that is reflected on the object is not possible due to compression artefacts in the low-resolution scan. Clear magnification would be possible with a higher resolution scan as it would reveal details of the roof more clearly. This would further serve to authenticate the picture by demonstrating that the reflection is indeed of the actual roof of the house.
The second problem we encounter is that of clearly showing a magnified image of the lower right corner of the print. This part of the picture serves to prove that the zigzag pattern is caused by uneven spreading of the processing chemicals and not by any manipulation of the picture. But again, magnification of the current low-resolution scan shows a degraded image. A high-resolution scan would more clearly show that the zigzag line was caused by the uneven spreading of the processing chemicals.
For these reasons, it would be most appreciated if the author of the photograph would allow us to do a higher resolution scan of the print so that we may demonstrate unequivocally that the photograph is genuine.
.
A Re-evaluation of the Balwyn UFO Photograph
By Francois Beaulieu
Introduction:
On April 2, 1966, at about two in the afternoon, a young Australian businessman by the name of James Kibel went outside of his house to take a few pictures. He owned an early Polaroid camera loaded with instant roll film that hadn't been used in a couple of years. The film was long past its expiry date, but he thought he'd nonetheless try and finish the roll by taking a few snapshots in his garden.
However, shortly after he went out, his attention was drawn to something unusual in the sky. He observed a silver metallic object that rapidly came in his direction and briefly hovered near his house. At that point, he had the presence of mind to raise his Polaroid camera and take a quick snapshot. The resulting picture soon ended up in various publications and holds the distinction today of being one of the most controversial UFO pictures ever taken.
This picture has been examined more or less closely over these many years and I had the recent opportunity to re-examine all that had been written about it and compare it against a recent scan of the actual print. This then is my re-evaluation of the Balwyn photograph.
My background
I became interested in UFOs at age six (in 1960). At age 8, I got my first UFO book. It contained several very realistic photomontages to illustrate some of the cases presented. At the time, I wasn't quite sure what photomontages were, but I could tell that there was something not quite right about those images. From that point on, I became suspicious of any photograph claimed to be that of a real UFO…
In the summer of 1967, I set out to do a series of tests to see if I could reproduce some of the UFO photographs I saw in popular UFO magazines of the period. My father happened to own a Polaroid Land 100 camera and I decided to use it to conduct the tests.
Polaroid Land film was the "peel-apart type". This was a type of film that contained the processing chemicals in a pocket at one end that was spread over the photographic paper when the film was pulled through two rollers at the side of the camera. I shot quite a lot of pictures using this camera during that time - not only of UFO models, but also of family members. And I still have these to this day. Thus, I am quite familiar with the behaviour of Polaroid film of that period. Flaws in the prints were very common due to the unpredictability of the film processing. Variations in temperature, how fast the film was pulled out of the camera and how the film was peeled apart could all affect the final appearance of the print.
The camera my father owned:

The peel-apart film:

One of my photos taken in August 1967 of a small UFO model (note the print flaws):

My experiments with the Polaroid camera eventually led to a lifelong passion for photography, which eventually led to research in three-dimensional media, which became my specialty up to the present day.
The Balwyn picture
I first came across the Balwyn picture shortly after it was taken. In those days, I visited newsstands quite regularly in search of any magazine that contained articles on UFOs and one day, I was amazed to find a special issue on the subject released by the well-known American magazine "LOOK". This was in 1967. This special issue (titled appropriately enough "Flying Saucers") contained several colour photographs of UFOs and, on page 34 appeared one particularly intriguing daylight picture showing an airborne object shaped like a bowl on its side and having a golden shade. The object appeared to be hovering over a house. I remember being fascinated by the picture but not having any opinions as to its authenticity. The picture was said to come from an anonymous source and looked fairly clear and sharp.


Many years later, looking back at this picture (yes, I still have a copy of that magazine in my files), I realize now that the reason why the object looked gold was most likely because it was a snapshot taken of the original print with daylight film under tungsten lighting.
Over the years, I saw the Balwyn picture reproduced multiple times in various magazines, mostly in black & white and in lower definition than the initial picture from LOOK magazine.
It was only a few years ago that I came across a better reproduction of this picture on Bill Chalker's website - thanks to a recent scan made of the original print. It showed the full image area in the original colours - revealing that the object was a silver colour, not the golden shade apparent on the original LOOK reproduction.

I was impressed to discover that the person who had taken that picture was now identified, was still alive and still had the original print in his possession.
I thus decided to do more research on this print and soon discovered that it was considered quite controversial. One of the points that was brought up was that one could see a reflection of the roof of a house on the surface of the object. According to the person who brought this up, this was, in his opinion, proof that the object was close to the photographer since he reasoned that the person taking the photograph was on the same side of the house as the object. In his opinion, the object was then most likely a very small object close to the camera.

The next controversy that was brought up was that there was what looked like a zigzag pattern or line of discontinuity on the original print, which some claimed was an indication that the picture was in fact a second generation photograph showing a composite of two distinct pictures.

So let's address the first point:
At the time when it was realized that the surface of the object reflected the roof of a house, we had not found the actual location where the picture was taken. After the actual house was located and that satellite pictures of it were examined, it was realized that the only way for that picture to have been taken was for the object to be on one side of the house and the photographer to be on the other side of the same house. This is because the object reflects one side of the house, but the roof and chimney that appear in the lower portion of the picture are of that same house, which means that the photographer had to be on the other side. The initial argument was based on the premise that the photographer was on the same side of the house as the object (and therefore the object may have been close to the photographer) and that the roof and chimney appearing at the bottom of the picture were that of a neighbouring house. But that has proven not to be the case.
It was also suggested by some that, although the photographer was clearly located on the left side of the house, the object might have been a small object on the same side and the reflection could be that of a house behind the photographer. However we found no such house in that location.
The reflection of the house appearing on the object and the roof and chimney appearing at the bottom of the picture are clearly of the same house. This means that the object had to be some distance away from the photographer and thus had to be fairly large…

Comparing Paul Dean's picture of the roof of the house from the left side with the roof as it appears in the original picture:

Now let's address the second point:
Several people pointed to a zigzag line that appears about the middle of the picture and seems to delineate what looks like a difference in exposure between the top and bottom of the picture. This apparent difference takes the form of a slightly greyish cast on the top part of the picture and is most apparent on the recent scan made of the print.
Some have suggested that this proves that the Balwyn photograph is in fact a composite of two pictures that were cut with a pair of jagged-edged scissors and glued together.
This explanation is questionable for a number of reasons. First of all, Polaroid prints of the period tended to warp very rapidly. They would warp within minutes of being laid flat on a table. It would have been very difficult to mount two such prints and not reveal their cut edges quite clearly. In fact, even with a normal print, the edges of each image would still be very clearly defined.
I in turn suggested that a similar effect might have more easily been produced using a double exposure technique. Polaroid cameras of that period were designed in such a way that more than one exposure could be made before the film was pulled out of the camera for processing. Thus, a lens cap with a zigzag pattern cut-out could in theory have been used to accomplish such an effect.
However, even if either of the above techniques had been attempted, there would have been a major hurdle in creating such a hoax: As was mentioned above, the object in the picture reflects back into the camera's lens an image of the roof of the house. To create a hoax, a metallic bowl of sorts would have had to be thrown in the air and photographed just at the right moment. The likelihood that a bowl thrown up in the air would position itself in a way where it would reflect the roof of the house back into the lens of the camera is quite slim and could not be seen by the photographer until after the photograph was processed. Therefore, an enormous number of attempts would have had to be made in order to hopefully get a single picture that matches this requirement. This would have been quite a feat to accomplish. Yet the photographer himself never even brought up the matter of the object reflecting the roof of the house.
The problem with all the theories above (including my own) is that they do not match what actually appears on the scan of the print when it is examined closely.
One thing I knew from the days I used a Polaroid camera with peel-apart film was that the chemicals often spread unevenly on the print, which resulted in what looked like an unevenly exposed print. This became worse when the film had passed its expiry date, as the chemicals would tend to dry out and not spread over the entire length of the print.
Here is an example:

Looking closely at the scan of the Balwyn picture, it shows all the signs of a print that was exposed after its expiry date.
First, the top edge of the image shows a darker sky colour. Then there is that zigzag pattern suggesting that some chemicals had run out as the print was pulled out of the camera. Similar zigzag patterns have been observed on other Polaroid prints.
Here is an example:

On the Balwyn print, one can see that the top section (above the zigzag) has a greyish tinge. But what is most telling is that, at the bottom right edge of the print, one can see the greyish chemicals widening up again as they reach the right edge and then completely run out. The characteristic observed at the bottom right edge effectively proves that the zigzag line was indeed caused by the chemical spreading unevenly and not by any manipulation of the print or of the exposure.

Now, compare this to (where the chemicals similarly run out completely at one edge):

Other observations
I would like to add here that the claim of this being a photograph of a photomontage is weakened even more when one examines the camera used to take the picture.

In order to photograph a photomontage, a very precise alignment and focusing of the camera is necessary. The problem here is that a camera such as the Polaroid 800 does not have a viewfinder that allows such alignment and focus at close range due to the wide parallax discrepancies between the lens position and the viewfinder position. Therefore, it would have been extremely difficult to align and focus such a camera on a small composite made up of two prints - not to mention properly lighting it.
One could of course suggest that the original is not a Polaroid print. However, the current scan shows all the flaws typical of Polaroid prints of the period - flaws that did not appear on regular processed prints. Also, a recent scan showing the jagged edges of the print proves that the original print is indeed of the type used in Polaroid 800 cameras, which the photographer says he used. The film name is Polaroid Land Picture roll type 48.

Here a scan of the Balwyn print showing the jagged edges typical of Polaroid roll film compared to a period print made with the same Polaroid roll film (in its b&w version - type 47):


Therefore it is clearly established that the original Balwyn print was made using Polaroid roll film of the period which can only be loaded in specific early sixties Polaroid roll film cameras such as the model 800. None of these models had features that would allow easy photo duplication or manipulation.
Another point worth noting: When the witness saw the object, he described it as being in an upright position. However, just as he was about to take the picture, he claims that the object unexpectedly flipped on its side and, as soon as the picture was taken, it flipped back to its original orientation. This bizarre manoeuvre puzzled the witness. Yet it is in fact the reason why the surface of the object in the picture reflects the roof of the house. Had the object remained in an upright position while the picture was taken, it would have only reflected the sky and clouds above it and thus, no clue would have appeared on the picture as to its distance from the camera.
Conclusion
I have no doubt after studying the scan of this print for over a year that the picture is a single exposure of the actual scene taken with a Polaroid camera dating from the early sixties and that the object in the picture was airborne and most likely of significant size. Of course, the nature and origin of the object remain unknown.
Taking the analysis further
One problem we have at the moment is that the scan of the original print is of low resolution and in a compressed format (jpg). We would need a scan to be from eight to sixteen times higher resolution and in uncompressed format (tif or bmp) in order to reveal more detail in the print.
The first problem we encounter with the current scan is that magnification of the image that is reflected on the object is not possible due to compression artefacts in the low-resolution scan. Clear magnification would be possible with a higher resolution scan as it would reveal details of the roof more clearly. This would further serve to authenticate the picture by demonstrating that the reflection is indeed of the actual roof of the house.
The second problem we encounter is that of clearly showing a magnified image of the lower right corner of the print. This part of the picture serves to prove that the zigzag pattern is caused by uneven spreading of the processing chemicals and not by any manipulation of the picture. But again, magnification of the current low-resolution scan shows a degraded image. A high-resolution scan would more clearly show that the zigzag line was caused by the uneven spreading of the processing chemicals.
For these reasons, it would be most appreciated if the author of the photograph would allow us to do a higher resolution scan of the print so that we may demonstrate unequivocally that the photograph is genuine.
.






